[Closed] finding UV coordinates on mesh
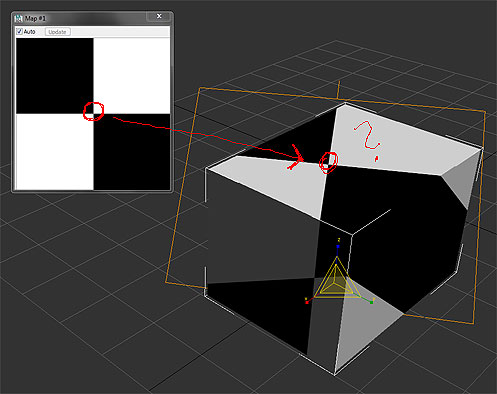
Hi,
I’m fighting with UVW again.
This time I want to find a given UV position (for example 0.5/0.5, as in the image) on a surface, to create a vertex, or slice along a given line.
Anyone got an idea how to do it? I know how to find a map vertex position, but this time I want to find positions where there are no map vertices.
not done it but my approach would probably be; find out which uvface the UV coordinate resides in, then compute the Barycentric coordinates for that point in that face… then use those coordinates to calculate the vertex position in the mesh face. If you look up “point in triangle” in google should get you all the info you need.
Yes that sounds good.
I’ll figure out the barycentric coordinates stuff.
Where I’m stuck is the first step, I have no idea yet how to find the corresponding UV face(s) for a given UV coordinate.
Thanks for the link.
I tried to put that into a script but no success yet.
I don’t quite understand yet how this algorithm is supposed to work, but I’m getting closer…
(
local meshObj = $Plane001
local theChannel=1
local UVsearch=[0.25,0.4]
--collect all faces
local meshFaces=meshObj.faces as bitarray
--collect all verts for each face
theMapFaces=for f in meshFaces collect meshop.getMapFace meshObj theChannel f
--collect UV coords of each face/vertex
theFaceVertsUVCoords=for v in theMapFaces collect
(
#(meshop.getMapVert meshObj theChannel v.x, meshop.getMapVert meshObj theChannel v.y, meshop.getMapVert meshObj theChannel v.z)
)
--Check if point is in triangle
for f in theFaceVertsUVCoords do
(
A=f[1]
B=f[2]
C=f[3]
u=UVsearch.x
v=UVsearch.y
P = A + u * (C - A) + v * (B - A)
--Compute vectors
v0 = C - A
v1 = B - A
v2 = P - A
--Compute dot products
dot00 = dot v0 v0
dot01 = dot v0 v1
dot02 = dot v0 v2
dot11 = dot v1 v1
dot12 = dot v1 v2
--Compute barycentric coordinate
invDenom = 1.0 / (dot00 * dot11 - dot01 * dot01)
u = (dot11 * dot02 - dot01 * dot12) * invDenom
v = (dot00 * dot12 - dot01 * dot02) * invDenom
--Check if point is in triangle
result=(u > 0) and (v > 0) and (u + v < 1)
format "A:% B:% C:% u:% v:% result:%
" A B C u v result
)
)
output:
A:[0,0.25,0] B:[0,0,0] C:[0.25,0.25,0] u:0.25 v:0.4 result:true
A:[0.25,0,0] B:[0.25,0.25,0] C:[0,0,0] u:0.25 v:0.4 result:true
A:[0.25,0.25,0] B:[0.25,0,0] C:[0.5,0.25,0] u:0.25 v:0.4 result:true
A:[0.5,0,0] B:[0.5,0.25,0] C:[0.25,0,0] u:0.25 v:0.4 result:true
A:[0.5,0.25,0] B:[0.5,0,0] C:[0.75,0.25,0] u:0.25 v:0.4 result:true
A:[0.75,0,0] B:[0.75,0.25,0] C:[0.5,0,0] u:0.25 v:0.4 result:true
A:[0.75,0.25,0] B:[0.75,0,0] C:[1,0.25,0] u:0.25 v:0.4 result:true
A:[1,0,0] B:[1,0.25,0] C:[0.75,0,0] u:0.25 v:0.4 result:true
A:[0,0.5,0] B:[0,0.25,0] C:[0.25,0.5,0] u:0.25 v:0.4 result:true
A:[0.25,0.25,0] B:[0.25,0.5,0] C:[0,0.25,0] u:0.25 v:0.4 result:true
A:[0.25,0.5,0] B:[0.25,0.25,0] C:[0.5,0.5,0] u:0.25 v:0.4 result:true
A:[0.5,0.25,0] B:[0.5,0.5,0] C:[0.25,0.25,0] u:0.25 v:0.4 result:true
A:[0.5,0.5,0] B:[0.5,0.25,0] C:[0.75,0.5,0] u:0.25 v:0.4 result:true
A:[0.75,0.25,0] B:[0.75,0.5,0] C:[0.5,0.25,0] u:0.25 v:0.4 result:true
A:[0.75,0.5,0] B:[0.75,0.25,0] C:[1,0.5,0] u:0.25 v:0.4 result:true
A:[1,0.25,0] B:[1,0.5,0] C:[0.75,0.25,0] u:0.25 v:0.4 result:true
A:[0,0.75,0] B:[0,0.5,0] C:[0.25,0.75,0] u:0.25 v:0.4 result:true
A:[0.25,0.5,0] B:[0.25,0.75,0] C:[0,0.5,0] u:0.25 v:0.4 result:true
A:[0.25,0.75,0] B:[0.25,0.5,0] C:[0.5,0.75,0] u:0.25 v:0.4 result:true
A:[0.5,0.5,0] B:[0.5,0.75,0] C:[0.25,0.5,0] u:0.25 v:0.4 result:true
A:[0.5,0.75,0] B:[0.5,0.5,0] C:[0.75,0.75,0] u:0.25 v:0.4 result:true
A:[0.75,0.5,0] B:[0.75,0.75,0] C:[0.5,0.5,0] u:0.25 v:0.4 result:true
A:[0.75,0.75,0] B:[0.75,0.5,0] C:[1,0.75,0] u:0.25 v:0.4 result:true
A:[1,0.5,0] B:[1,0.75,0] C:[0.75,0.5,0] u:0.25 v:0.4 result:true
A:[0,1,0] B:[0,0.75,0] C:[0.25,1,0] u:0.25 v:0.4 result:true
A:[0.25,0.75,0] B:[0.25,1,0] C:[0,0.75,0] u:0.25 v:0.4 result:true
A:[0.25,1,0] B:[0.25,0.75,0] C:[0.5,1,0] u:0.25 v:0.4 result:true
A:[0.5,0.75,0] B:[0.5,1,0] C:[0.25,0.75,0] u:0.25 v:0.4 result:true
A:[0.5,1,0] B:[0.5,0.75,0] C:[0.75,1,0] u:0.25 v:0.4 result:true
A:[0.75,0.75,0] B:[0.75,1,0] C:[0.5,0.75,0] u:0.25 v:0.4 result:true
A:[0.75,1,0] B:[0.75,0.75,0] C:[1,1,0] u:0.25 v:0.4 result:true
A:[1,0.75,0] B:[1,1,0] C:[0.75,0.75,0] u:0.25 v:0.4 result:true
result:true for everything is wrong…
isn’t P just the UV coordinate ?
fn PointInTriangle A B C pnt &u &v &w =
(
v0 = C - A
v1 = B - A
v2 = pnt - A
-- Compute dot products
dot00 = dot v0 v0;
dot01 = dot v0 v1;
dot02 = dot v0 v2;
dot11 = dot v1 v1;
dot12 = dot v1 v2;
-- Compute barycentric coordinates
invDenom = 1 / (dot00 * dot11 - dot01 * dot01)
u = (dot11 * dot02 - dot01 * dot12) * invDenom
v = (dot00 * dot12 - dot01 * dot02) * invDenom
w = 1 - (u + v);
-- Check if point is in triangle
(u > 0) and (v > 0) and (u + v < 1);
)
still no luck, but now I used the “slower” method described on the site:
(
local meshObj = $Plane001
local theChannel=1
local UVsearch=[0.02,0.019,0]
--collect all faces
local meshFaces=meshObj.faces as bitarray
--collect all verts for each face
theMapFaces=for f in meshFaces collect meshop.getMapFace meshObj theChannel f
--collect UV coords of each face/vertex
theFaceVertsUVCoords=for v in theMapFaces collect
(
#(meshop.getMapVert meshObj theChannel v.x, meshop.getMapVert meshObj theChannel v.y, meshop.getMapVert meshObj theChannel v.z)
)
function SameSide p1 p2 a b = dot (cross (b-a) (p1-a)) (cross (b-a) (p2-a))>=0
function PointInTriangle p a b c = (SameSide p a b c) and (SameSide p b a c) and (SameSide p c a b)
--collect all affected faces
hitFaces=for f in theFaceVertsUVCoords collect PointInTriangle UVsearch f[1] f[2] f[3] --Check if point is in triangle
for f=1 to hitFaces.count where hitFaces[f]==true do
(
print f
)
)
It works!
I can find all faces “touched” by a specific UV position.
But what I really need is to convert the UV position to barycentric coordinates of that face.
Sounds easy, but how?
EDIT: think I have figured out the whole thing…will post the solution later…
I think it isn’t much difficult, but take some hours to make that script.
From a 2D point in UV, you can find all UV faces containing that point.
Depend on their relative postion in that UV face you can calculate the real postion in 3D
Hi Batigol,
Thanks for your interest.
I’m almost there, the result is in a new thread: