[Closed] Find visual center of contour/polygon
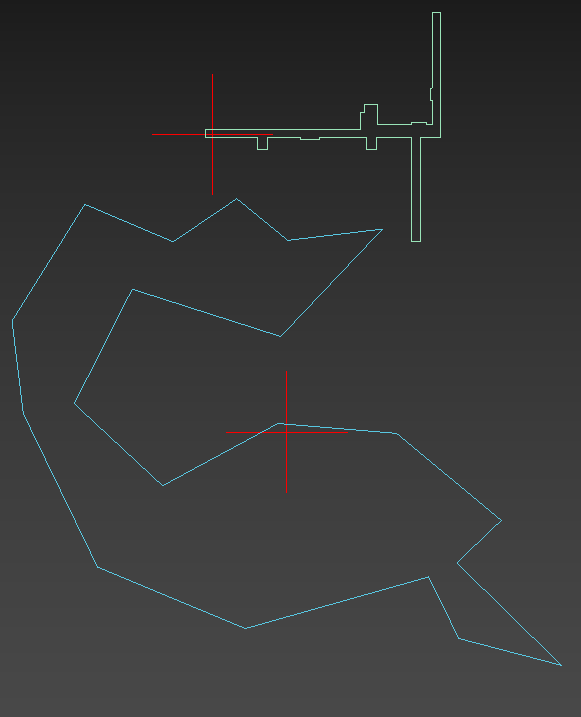
What I am trying to achieve is to find a visual center of a closed shape(polygon).
Maybe the best approach is this one: https://blog.mapbox.com/a-new-algorithm-for-finding-a-visual-center-of-a-polygon-7c77e6492fbc
Here is the source code: https://github.com/mapbox/polylabel
I have spent some time to “convert” the javascript version into maxscript version, but I don’t get the same result as the original code.
Red points are the result I have:
I am pretty sure that my code is not “converted” properly.
There are few c# implementations of the Polylabel:
So, my question is – can these c# versions be “converted” so to be used inside maxscript?
Did you try the original js code with your points data? Does it produce the result you would expect?
.
.
upd
You can compile it in maxscript as usual and use PolyLabel.GetPoleOfInaccessibility method. It expects two arrays of X and Y polygon point coords and the precision value.
Guess it would be easier to convert that to maxscript then the original js version.
void Main()
{
var x = new double[]{-137.422, -62.9051, 6.80396, 127.393, 128.194, 69.3018, -0.807953, -50.0851, -58.0976, -6.0161, 65.2955, 123.787, 178.673, 170.66, 134.203, 28.4378, -68.1133, -133.415};
var y = new double[]{22.4472, 93.3582, 112.188, 106.98, 67.3175, 70.5225, 65.7149, 41.6773, -10.0036, -40.0506, -2.39166, -10.8048, -88.5265, -143.412, -170.254, -162.642, -129.791, -41.2525};
var pt = PolyLabel.GetPoleOfInaccessibility( x, y, 1.0f );
Console.WriteLine( pt );
}$Point_Helper:Point001 @ [16.486824,-100.195145,0.000000]
public class MapPoint
{
public double X;
public double Y;
public MapPoint( double x, double y )
{
X = x;
Y = y;
}
}
// Define other methods and classes here
public class Cell
{
public double X { get; set; }
public double Y { get; set; }
public double Half { get; set; }
public double Distance { get; set; }
public double Max { get; set; }
public Cell(double x, double y, double half, List<List<MapPoint>> polygon)
{
X = x;
Y = y;
Half = half;
Distance = Adjunct.PointToPolygonDistance(x, y, polygon);
Max = Distance + Half * Math.Sqrt(2);
}
}
public class CellMaxComparer : IComparer<Cell>
{
public int Compare(Cell x, Cell y)
{
return x.Max.CompareTo(y.Max);
}
}
public static class Adjunct
{
public static double PointToPolygonDistance(double x, double y, List<List<MapPoint>> polygon)
{
bool inside = false;
double minDistSq = double.MaxValue;
for (int k = 0; k < polygon.Count; k++)
{
List<MapPoint> ring = polygon[k];
int count = ring.Count;
int j = count - 1;
for (int i = 0; i < count; j = i++)
{
MapPoint a = ring[i];
MapPoint b = ring[j];
if (((a.Y > y) != (b.Y > y)) && (x < ((b.X - a.X) * (y - a.Y) / (b.Y - a.Y + a.X))))
{
inside = !inside;
}
minDistSq = Math.Min(minDistSq, GetSegDistSq(x, y, a, b));
}
}
return (inside ? 1 : -1) * Math.Sqrt(minDistSq);
}
public static double GetSegDistSq(double px, double py, MapPoint a, MapPoint b)
{
var x = a.X;
var y = a.Y;
var dx = b.X - x;
var dy = b.Y - y;
if (dx != 0 || dy != 0)
{
var t = ((px - x) * dx + (py - y) * dy) / (dx * dx + dy * dy);
if (t > 1)
{
x = b.X;
y = b.Y;
}
else if (t > 0)
{
x += dx * t;
y += dy * t;
}
}
dx = px - x;
dy = py - y;
return dx * dx + dy * dy;
}
}
static class PolyLabel
{
public static double[] GetPoleOfInaccessibility( double[] x, double[] y, float precision )
{
var lst = new List<List<MapPoint>>{ new List<MapPoint>() };
for ( int i = 0; i < x.Length; i++ )
{
lst[0].Add( new MapPoint( x[i], y[i] ) );
}
var result = PoleOfInaccessibility( lst, precision );
return new double[]{ result.Item1, result.Item2 };
}
public static Tuple<double, double> PoleOfInaccessibility(List<List<MapPoint>> polygon, double precision = 1.0, bool debug = false)
{
double minY = double.MaxValue;
double maxY = double.MinValue;
double minX = double.MaxValue;
double maxX = double.MinValue;
for (int i = 0; i < polygon[0].Count; i++)
{
MapPoint p = polygon[0][i];
if (p.X < minX) minX = p.X;
if (p.Y < minY) minY = p.Y;
if (p.X > maxX) maxX = p.X;
if (p.Y > maxY) maxY = p.Y;
}
double width = maxX - minX;
double height = maxY - minY;
double cellSize = Math.Min(width, height);
double half = cellSize / 2;
List<Cell> cellList = new List<Cell>();
CellMaxComparer comp = new CellMaxComparer();
if (cellSize == 0)
{
return Tuple.Create<double, double>(minX, minY);
}
for (double x = minX; x < maxX; x += cellSize)
{
for (double y = minY; y < maxY; y += cellSize)
{
cellList.Add(new Cell(x + half, y + half, half, polygon));
}
}
cellList.Sort(comp);
Console.WriteLine(string.Format("first sort"));
cellList.ForEach(delegate (Cell queueCell)
{
Console.WriteLine(string.Format("{0}, {1}, {2}, {3}, {4}", queueCell.X, queueCell.Y, queueCell.Half, queueCell.Distance, queueCell.Max));
});
Cell bestCell = GetCentroidCell(polygon);
Cell bboxCell = new Cell(minX + width / 2, minY + height / 2, 0, polygon);
if (bboxCell.Distance > bestCell.Distance)
{
bestCell = bboxCell;
}
int numProbes = cellList.Count;
while (cellList.Count != 0)
{
Console.WriteLine(string.Format("cellQueue.Count = {0}", cellList.Count));
cellList.ForEach(delegate (Cell queueCell)
{
Console.WriteLine(string.Format("{0}, {1}, {2}, {3}, {4}", queueCell.X, queueCell.Y, queueCell.Half, queueCell.Distance, queueCell.Max));
});
int i = cellList.Count - 1;
Cell cell = cellList[i];
cellList.RemoveAt(i);
if (cell.Distance > bestCell.Distance)
{
bestCell = cell;
Console.WriteLine(string.Format("found best {0} after {1} probes", Math.Round(1e4 * cell.Distance) / 1e4, numProbes));
}
if (cell.Max - bestCell.Distance <= precision) continue;
Console.WriteLine(string.Format("add four more"));
half = cell.Half / 2;
cellList.Add(new Cell(cell.X - half, cell.Y - half, half, polygon));
cellList.Add(new Cell(cell.X + half, cell.Y - half, half, polygon));
cellList.Add(new Cell(cell.X - half, cell.Y + half, half, polygon));
cellList.Add(new Cell(cell.X + half, cell.Y + half, half, polygon));
cellList.Sort(comp);
numProbes += 4;
}
Console.WriteLine("num probes: " + numProbes);
Console.WriteLine("best distance: " + bestCell.Distance);
return Tuple.Create<double, double>(bestCell.X, bestCell.Y);
}
public static Cell GetCentroidCell(List<List<MapPoint>> polygon)
{
double area = 0;
double x = 0;
double y = 0;
List<MapPoint> points = polygon[0];
int count = points.Count;
int j = count - 1;
for (int i = 0; i < count; j = i++)
{
MapPoint a = points[i];
MapPoint b = points[j];
double f = a.X * b.Y - b.X * a.Y;
x += (a.X + b.X) * f;
y += (a.Y + b.Y) * f;
area += f * 3;
}
if (area == 0)
{
return new Cell(points[0].X, points[0].Y, 0, polygon);
}
return new Cell(x / area, y / area, 0, polygon);
}
}Yep. I have “converted” the original js code to maxscript. The image in my first post shows the result – not what I expect. But, I am pretty sure that this “conversion” is not right.
You can compile it. I can’t.
just find any example of compiled on the fly .net class on this forum. User32 or anything like that…
You don’t need Main method so you can delete it.
Compile the source and access the method like this (dotnetclass “Test.PolyLabel”).GetPoleOfInaccessibility
here’s a .net playground. you can put your values to Main method to test if it really works
https://dotnetfiddle.net/1OvSDX
wish I could help but after looking at the c++ source, I’m ooot that’s just some nasty nasty coding. Look around for another implementation would be my suggestion.
There are few python implementation but in all of them the code is almost the same.
@Serejah, does the image you posted above is from the same code(polylabel) used inside 3ds max?
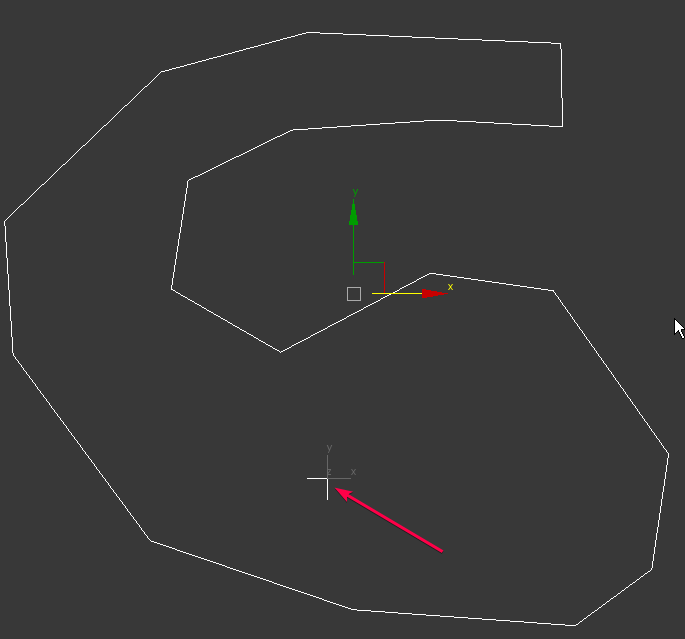
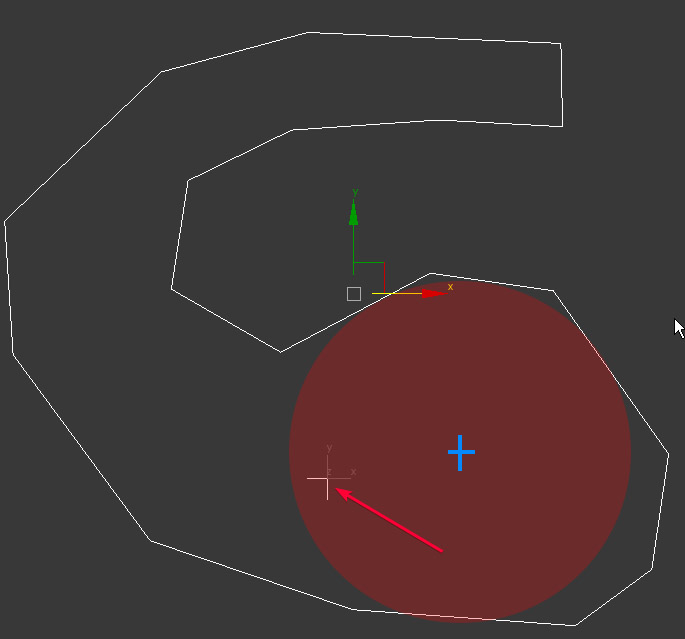
I am not sure, but I think that the proper point has to be the one marked with blue:
Or this is another way to solve the problem – finding the largest inscribed circle.
Totally agree with you. Maybe this c# version is not a great port of js version. You have to compare both of them with same values to see.
ps I didn’t compile it in max, just used the knot pos values from spline in .net playground to calc the coords
I haven’t done a pure MXS in a while, but let’s see if I’ve lost my skills
global MapBoxOps
(
struct MapBoxStruct
(
cell =
(
struct cell
(
private
FLT_MAX = 3.40282e+038,
SQRT2 = sqrt(2),
public
center,
h = 0,
d = 0,
maxdist = FLT_MAX,
fn getSegDistSq p a b =
(
x = a.x
y = a.y
dx = b.x - x
dy = b.y - y
if (dx != 0 or dy != 0) do
(
t = ((p.x - x) * dx + (p.y - y) * dy) / (dx * dx + dy * dy)
if (t > 1) then
(
x = b.x
y = b.y
)
else if (t > 0) do
(
x += dx * t
y += dy * t
)
)
dx = p.x - x
dy = p.y - y
dx * dx + dy * dy
),
fn pointToPolygonDist point polygon =
(
inside = false
minDistSq = FLT_MAX
for ring in polygon do
(
for i = 1 to ring.count do
(
a = ring[i]
b = if i == ring.count then ring[1] else ring[i+1]
if ((a.y > point.y) != (b.y > point.y) and (point.x < (b.x - a.x) * (point.y - a.y) / (b.y - a.y) + a.x)) do inside = not inside
minDistSq = amin minDistSq (getSegDistSq point a b)
)
)
(sqrt minDistSq) * (if inside then 1 else -1)
),
fn getDist polygon =
(
d = pointToPolygonDist center polygon
maxdist = d + h * SQRT2 --- here was a bug!
)
)
),
bbox =
(
struct bbox
(
bmin = FLT_MAX * [1,1,1],
bmax = -FLT_MAX * [1,1,1],
fn size = (bmax - bmin)
)
),
fn makeBBox points =
(
b = bbox()
for p in points do for i=1 to 3 do
(
if p[i] < b.bmin[i] do b.bmin[i] = p[i]
if p[i] > b.bmax[i] do b.bmax[i] = p[i]
)
b
),
fn makeCell center h polygon =
(
c = cell center:center h:h
c.getDist polygon
c
),
fn getCentroidCell polygon =
(
area = 0
c = [0,0,0]
ring = polygon[1]
for i = 1 to ring.count do
(
a = ring[i]
b = if i == ring.count then ring[1] else ring[i+1]
f = a.x * b.y - b.x * a.y
c.x += (a.x + b.x) * f
c.y += (a.y + b.y) * f
area += f * 3
)
center = if area == 0 then ring[1] else c/area
makeCell center 0 polygon
),
fn cellSorter c1 c2 = if c1.maxdist < c2.maxdist then -1 else if c1.maxdist > c2.maxdist then 1 else 0,
fn polyLabel polygon precision:1 debug:false =
(
-- find the bounding box of the outer ring
bb = makeBBox polygon[1]
size = bb.size()
cellSize = amin size.x size.y
if (cellSize == 0) do return bb.bmin
h = cellSize / 2
-- a priority queue of cells in order of their "potential" (max distance to polygon)
-- using cellSorter
-- cover polygon with initial cells
cells = #()
for x = bb.bmin.x to bb.bmax.x by cellSize do
(
for y = bb.bmin.y to bb.bmax.y by cellSize do
(
append cells (makeCell [x + h, y + h, 0] h polygon)
)
)
-- take centroid as the first best guess
bestCell = getCentroidCell polygon
-- second guess: bounding box centroid
bboxCell = makeCell (bb.bmin + size/2.0) 0 polygon
if (bboxCell.d > bestCell.d) do
(
bestCell = bboxCell
)
numProbes = cells.count
while cells.count != 0 do
(
-- pick the most promising cell from the queue
qsort cells cellSorter
currCell = cells[cells.count]
cells.count = cells.count - 1
-- update the best cell if we found a better one
if (currCell.d > bestCell.d) do
(
bestCell = currCell
if (debug) do format "found best % after % probes\n" currCell.d numProbes
)
-- do not drill down further if there's no chance of a better solution
if (currCell.maxdist - bestCell.d > precision) do
(
-- split the cell into four cells
h = currCell.h/2
append cells (makeCell [currCell.center.x - h, currCell.center.y - h, 0] h polygon)
append cells (makeCell [currCell.center.x + h, currCell.center.y - h, 0] h polygon)
append cells (makeCell [currCell.center.x - h, currCell.center.y + h, 0] h polygon)
append cells (makeCell [currCell.center.x + h, currCell.center.y + h, 0] h polygon)
numProbes += 4
)
)
if (debug) do
(
format "num probes: %\n" numProbes
format "best distance: %\n" bestCell.d
)
bestCell.center
)
)
MapBoxOps = MapBoxStruct()
ok
)
/*
MapBoxOps.polyLabel <array><array of points>polygon
*/
I didn’t do any optimization (just ported c++ code from the first post)… I’m sure it might be optimized
Talking about precision parameter in this algorithm… I guess that there is no reason to set it less than a half of minimum distance between two ring (spline) points. What do you think?
Thanks, Denis. It works!
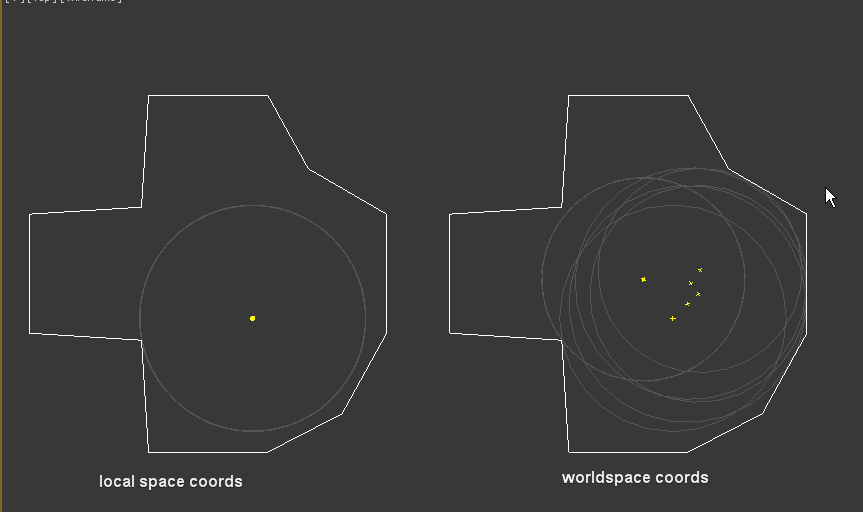
Although the result depends on what coordspace we use (and it is expected).
I did ten 36° rotations to collect results and I guess the best result would be the average of these worldspace results? In this case precision shouldn’t matter much
Thank you, Denis.
Reading your code and using part of it I was able to fix mine. This is the difference, but it is essential:
qsort cellQueue cellSorter
Here is the results that I have – green points are generated from your code, yellow – from mine.
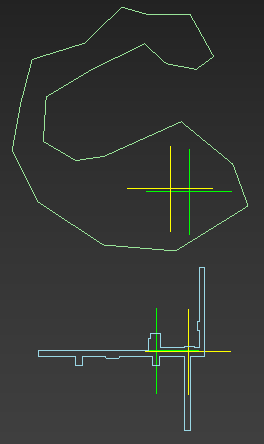
On the top shape I think that the yellow point is placed more correctly, but on the bottom shape the green point is placed more correctly.
The difference of placement is because in the js code which I have used the maxDist is calculated this way
maxdist = d + cellH * sqrt2
while, in your code it is calculated this way
maxdist = amax d (h * sqrt2)
Using the same calculation in both codes produces the same result.
I don’t know why but your code finds the green point in the bottom shape for ~1.1 sec, while the js version takes ~0.06 sec(using maxdist = d + cellH * sqrt2 ) and ~0.45 sec(using maxdist = amax d (h * sqrt2)).
Here is my version of the js code:
(
function Get_seg_dist_sq px py a b =
(
x = a.x
y = a.y
dx = b.x - x
dy = b.y - y
if dx != 0 or dy != 0 do
(
t = ((px - x) * dx + (py - y) * dy) / (dx * dx + dy * dy)
if t > 1 then
(
x = b[1]
y = b[2]
)
else
(
if t > 0 do
(
x += dx * t
y += dy * t
)
)
)
dx = px - x
dy = py - y
dx * dx + dy * dy
)
function PointToPolygonDist x y polygon =
(
inside = false
min_dist_sq = 1e9
for k = 1 to polygon.count do
(
a = polygon[k]
b = if k == polygon.count then polygon[1] else polygon[k + 1]
if ((a[2] > y) != (b[2] > y) and (x < (b[1] - a[1]) * (y - a[2]) / (b[2] - a[2]) + a[1])) do
inside = not inside
min_dist_sq = amin #(min_dist_sq, Get_seg_dist_sq x y a b)
)
result = sqrt (min_dist_sq)
if not inside then -result else result
)
local sqrt2 = sqrt 2
function Cell centerX centerY cellH polygon =
(
d = PointToPolygonDist centerX centerY polygon
-- js code
maxx = d + cellH * sqrt2
-- "denisT"
-- maxx = amax #(d, cellH * sqrt2)
#(centerX,centerY,cellH,d,maxx)
)
function GetCentroidCell polygon =
(
area1 = 0
x = 0
y = 0
for i = 1 to polygon.count do
(
a = polygon[i]
b = if i == polygon.count then polygon[1] else polygon[i+1]
f = a.x * b.y - b.x * a.y
x += (a.x + b.x) * f
y += (a.y + b.y) * f
area1 += f * 3
b = a
)
if area1 == 0 then
Cell polygon[1] polygon[2] 0 polygon
else
Cell (x / area1) (y / area1) 0 polygon
)
-- "denisT"
fn cellSorter c1 c2 = if c1[5] < c2[5] then -1 else if c1[5] > c2[5] then 1 else 0
function Polylabel polygon precision =
(
minX = 1e9
minY = 1e9
maxX = -1e9
maxY = -1e9
for p in polygon do
(
if p.x < minX do minX = p.x
if p.y < minY do minY = p.y
if p.x > maxX do maxX = p.x
if p.y > maxY do maxY = p.y
)
width = maxX - minX
height = maxY - minY
cellSize = amin #(width, height)
if (cellSize == 0) then
(
[minX, minY, 0]
)
else
(
h = cellSize / 2.0
cellQueue = #()
for x = minX to maxX by cellSize do
(
for y = minY to maxY by cellSize do
(
r = Cell (x + h) (y + h) h polygon
append cellQueue r
)
)
bestCell = GetCentroidCell polygon
bboxCell = Cell (minX + width / 2) (minY + height / 2) 0 polygon
if (bboxCell[4] > bestCell[4]) do bestCell = bboxCell
numProbes = cellQueue.count
cnt = 0
while (cellQueue.count) do
(
-- pick the most promising cell from the queue
qsort cellQueue cellSorter
cellM = cellQueue[cellQueue.count]
deleteItem cellQueue cellQueue.count
-- update the best cell if we found a better one
if (cellM[4] > bestCell[4]) do
(
bestCell = cellM
format "found best % after % probes\n" cellM[4] numProbes
)
-- do not drill down further if there's no chance of a better solution
if (cellM[5] - bestCell[4] <= precision) then
(
exit
)
else
(
-- split the cell into four cells
h = cellM[3] / 2
append cellQueue (Cell (cellM[1] - h) (cellM[2] - h) h polygon)
append cellQueue (Cell (cellM[1] + h) (cellM[2] - h) h polygon)
append cellQueue (Cell (cellM[1] - h) (cellM[2] + h) h polygon)
append cellQueue (Cell (cellM[1] + h) (cellM[2] + h) h polygon)
numProbes += 4
)
cnt += 1
if cnt > 10000 do exit
)
format "numProbes: % \n" numProbes
format "bestCell[4]: % \n" bestCell[4]
local poleOfInaccessibility = [bestCell[1], bestCell[2], bestCell[4]]
return poleOfInaccessibility
)
)
myPolygon = selection[1]
polygon = for k = 1 to numKnots myPolygon 1 collect
(
kPos = getKnotPoint myPolygon 1 k
[kPos.x, kPos.y,0]
)
t0 = timestamp()
rr = PolyLabel polygon 1
t1 = timestamp()
format "Time % sec.\n" ((t1-t0)/1000.0)
point pos:[rr[1],rr[2],0] wirecolor:yellow
format "rr: % \n" rr
)About precision:
-
when this is used
maxdist = d + cellH * sqrt2the precision value has an effect.
precision = 1 -> yellow point
precision = 0.1 -> blue point

-
when this is used
maxdist = amax d (h * sqrt2)the precision value has no effect.