[Closed] Bounding sphere for spheres

I’m going to explain it to you, although with little hope that you understand.
When I answer to you, I take my time to:

• Understand what your problem is
• Read and understand what your code does (you haven’t explained it).
• Think about your solution to see if it can be valid using all my mathematic-engineering background.
• Realize that it can’t and find a good example to show you that it can’t.
• Draw the example, capture the screen, upload the image to a server and post the answer.

After all that, the answer I recieve from you is that my example doesn’t fit what you are proposing. And that is not true. So, the only explanations I see are:

• You have taken a lot less time to read my post than me to try to give you a good answer. That is not very polite
• You don’t mind at all and you are going to use your method yes or yes. That is not very polite either.

By the way, you are lucky if your problem with the 183 pages PDF is just the English language. You have incredible Maths skill! Who could have said it…

Like I said, really apologize for the misunderstanding. I know it´s hard to believe, but english is really a much biger problem for me than math. I am defenetly not a Dr. of math, but the formula stuff, was the only thing, I more or less understood there.
But the biger problem then english language itself for me is its mentality (posiblly not the right word, but have no idea how to call it). When I write thanks for the answer, I meanI really greatfull and it shouldn´t be taken ironicaly, or don´t know how it called. It´s really hard for me to know how you´ll understand my answer.
So if I understood you right now, you think I wrote something like this: “your answer is sh*t, I don´t care about, going to use my solution aniway”. I defenetly didn´t said something like that.

here is a little toy to play with “bounding sphere” idea:

(
	/********** METHODS and STRUCTS ***********/
	struct SphereData (pair, radius, center)
	fn pairGenerator count = 
	(
		pairs = #()
		for k=1 to count do for n = (k+1) to count do append pairs [k,n]
		pairs
	)
	fn sphereDistance s0 s1 &center: = 
	(
		p = s1.pos - s0.pos
		d = length p
		v = normalize p
		p0 = s0.pos - s0.radius * v
		p1 = s1.pos + s1.radius * v
		if defined center do center = (p0 + p1)/2

		--point pos:p0
		--point pos:p1
		--point pos:center
		
		radius = (distance p0 p1)/2
		if radius < s0.radius or radius < s1.radius then -1 else radius
	)
	fn sortByRadius v0 v1 = if v0.radius < v1.radius then 1 else if v0.radius > v1.radius then -1 else 0

	/************ RANDOM SCENE SETUP ************/
	with redraw off
	(
		delete objects
		
		count = 50
		max_offset = 200
		minmax_radius = [5,100]
		
		for k=1 to count do 
		(
			pos = random -[max_offset,max_offset,max_offset] [max_offset,max_offset,max_offset]
			radius = random minmax_radius.x minmax_radius.y
			geosphere segs:8 pos:pos radius:radius name:(k as string) wirecolor:yellow
		)
		gc light:on
	)

	/********** MAKE BOUNDING SPHERE ***********/
	(
		bounds = #()
		iter = 0
		
		best_bound = -1
		curr_bound = 0
		
		act = on
		while act do
		(
			sps = for obj in objects where iskindof obj geosphere collect obj	
			ss = pairGenerator sps.count
			global _xx = for s in ss collect
			(
				x = s[1]
				y = s[2]
				r = sphereDistance sps[x] sps[y] center:&c
				
				SphereData pair:s radius:r center:c
			)
			qsort _xx sortbyradius
			p = _xx[1]
			curr_bound = p.radius
			if (best_bound + 0.01 < curr_bound) then
			(
				geosphere segs:8 radius:p.radius pos:p.center wirecolor:red name:#bound
				iter += 1
				best_bound = curr_bound
				
				append bounds best_bound
				format "% >> radius:%\n" iter best_bound
			)
			else act = off
		)

		format "% = difference:%\n" [bounds[1],bounds[iter]] (bounds[1]/bounds[iter]) 
		best_bound
	)
)

you can try to run whole script above.

it will make a scene of yellow target spheres and generate red bounding spheres for them.

in the listener you will see some log output which tells number of iterations, min and max bounding radius, and difference.

as you can see the difference is usually not greater than 10% depending on number of target spheres, their scattering size, and radius.

the algorithm idea is:
– find two the most distant spheres
– make a bounding sphere around these two
– add new bounding sphere to the target list
– repeat above steps…

the “ideal” bounding sphere is in-between first and last bounding spheres.
how to find it will be your homework

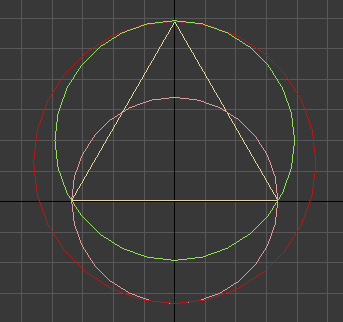
this is the worst possible difference (easy to calculate)

the red circle is the result of my algorithm, the green one is the “ideal” bounding…
the picture should give you a hint about how to find the “ideal”.

Thanks, that looks very interesting, let see what I can do with it using my very limited maxscript knowledge, but sincerely grateful.
Just 1 question, what is that other sphere is, I mean not the green and not the red one? No idea what that color is in english.