[Closed] Placing points along spline at even distance between them
I am sure that the title of the topic is not very accurate but this is my fault.
What I need is to place points on a spline and the points to be at even distance between them. I do not want the spline to be divided.
For example the first point to be at the same position of the first knot of the spline. The second point to lay on the spline but the straight distance to the first point to be 33 units. The third point to lay on the spline and the straight distance to the second point to be 33 units and so on.
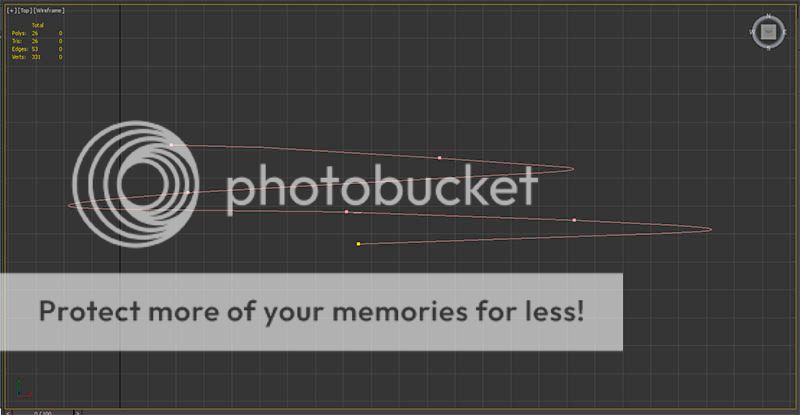
On the image below you can see what I mean:
https://drive.google.com/open?id=1ocbdZMAdPJlaua3rlup65T19fdgujCBn
The distance between the knots of the spline is 33 units(shown with green markers).
The code that I use to place the yellow points is:
curSpline = selection[1]
dist = 33.0
curvLength = curveLength curSpline ns
numSpl = numSplines curSpline
for ns = 1 to numSpl do
(
cnt = (floor (curvLength / dist)) as integer
for i = 0 to cnt do
(
point pos:(lengthInterp curSpline ns (i*dist/curvLength)) size:10
)
)And the result can be seen in the same image with yellow markers. As you see the distance between the points is not 33 units.
Is there are any easy way to place the points so the distance between them to be 33 units and all points to lays on the spline? Mathematical way. Or I have to use some dirty hacks to find the proper position of the points? What comes to my mind as a dirty hack is this:
(
curSpline = selection[1]
dist = 33.0
step = 1.0 / 1000000
stepPointsArr = for i = 0.0 to 1.0 by step collect (in coordsys world (interpCurve3D curSpline 1 i pathParam:false))
pointsPosArr = #()
stopLoop = false
firstPosIdx = 1
while stopLoop == false do
(
for j = firstPosIdx+1 to stepPointsArr.count do
(
if j != stepPointsArr.count then
(
curDist = distance stepPointsArr[firstPosIdx] stepPointsArr[j]
if abs (dist - curDist) < 0.001 do
(
append pointsPosArr stepPointsArr[j]
firstPosIdx = j
)
)
else
(
stopLoop = true
)
)
)
if pointsPosArr.count != 0 do
(
for p in pointsPosArr do
(
point pos:p wirecolor:yellow
)
)
)If you use the spline in this max(2014) file: https://drive.google.com/open?id=1FqZCp8VLfs8teEY1GHccltLpdR5PM1MR
the code above will create points almost at the same position where the knots of the splines are.
The only “Math” solution is intersecting the spline with a circle with the given radius and the last point as the center.
I’ve never used the shape intersect option in 3dsMax. You can try and see if it’s ok in performance.
I will think a little more about optimization… or by searching the math result.
Hi, aaandres.
Using a circle was my first idea, but finding the intersection between a circle and a “bezier” spline… I have a dirty solution for this task too.
I can test any new way of solving the problem on sunday evening. I have to go to the bed now. Tomorrow I am at work(24h shift).
This is definitely not a way to go if you want pure math solution, but anyway.
(
delete objects
delete helpers
shp = Ngon radius:50 cornerRadius:0 nsides:33 circular:on scribe:1
shp.steps = 50
noisemod = Noisemodifier strength:[30,30,0] scale:10.0
addModifier shp noisemod
convertToSplineShape shp
len = curveLength shp 1
step = 20.0 as double
h = for i=1 to 10 collect point centermarker:on cross:off wirecolor:yellow
param = step / len
format "PARAM: %\n" param
params = #()
gc();t1=timestamp();hf = heapfree
current = 0.0 as double
for i=1 to h.count - 1 do
(
p0 = lengthInterp shp 1 current steps:4444
p1 = lengthInterp shp 1 (current + param) steps:4444
while not keyboard.escPressed do
(
d = distance p0 p1
if (abs (d - step)) < 0.01 do
(
format "%: param:%\n" i current
append params current
exit
)
if d < step do
(
current = current + param * (mod (step / d) 1.0)
p1 = lengthInterp shp 1 current steps:44444
)
if d > step do
(
current = current - param * (1.0 - step / d)
p1 = lengthInterp shp 1 current steps:44444
)
)
)
format "Time: %sec. Mem: %\n" ((timestamp()-t1)/1000 as float) (hf-heapfree)
h[1].pos = lengthInterp shp 1 0 steps:44444
for i=1 to params.count do
(
h[i+1].pos = lengthInterp shp 1 params[i] steps:44444
)
)Wonder how could we do it similar to this approach
Pure Math solution is a sixth degree equation… thus we have to go through numerical solution.
The quickest should be Newton-Raphson, but we’ll have first to calculate the spline equation and then it’s derivative.
So, I think the best solution is just find the segment where the next point lies and then search it by bisection. We can use the more accurate function ‘interpBezier3D’ and, of course, use pathParam instead of lenghParam (faster and more accurate).
For your spline, Kostadin, I get 1 msec face to the 4 sec of the original solution with one more decimal precision. Not bad!
(
t1 = timeStamp()
curSpline = selection[1]
fixedDist = 33.0
accuracy = 0.0001
-- PathParam of each knot
numK = numknots curSpline
if isClosed curSpline 1 do numK +=1
invNumK = 1.0 / (numK - 1)
knotsParam = for i = 1 to numK collect invNumK * (i-1)
knotsArray = for i = 1 to numK collect (in coordsys world (interpCurve3D curSpline 1 knotsParam[i] pathParam:true))
pointsPosArr = #(knotsArray[1])
stopLoop = false
currentKnotIdx = 2
while stopLoop == false do
(
-- Find segment where the next point lies
lastPoint = pointsPosArr[pointsPosArr.count]
morePoints = false
for i = currentKnotIdx to numK while not morePoints do
(
dist = distance lastPoint knotsArray[i]
currentKnotIdx = i
if dist >= fixedDist do
(
morePoints = true
)
)
if morePoints then
(
-- Let's find the point by bisection in the segment found (max 1000 iterations)
pt
error = 1e6
a = 0.0
b = 1.0
iterations = 0
while error > accuracy and iterations < 1000 do
(
iterations += 1
param = (a+b) * 0.5
pt = interpBezier3D curSpline 1 (currentKnotIdx - 1) param pathParam:true
dist = distance lastPoint pt
if dist > fixedDist then b = param else a = param
error = abs(dist - fixedDist)
)
append pointsPosArr pt
)
else
(
stopLoop = true
)
)
t2 = timeStamp()
format "Time= %ms\n" (t2-t1)
for p in pointsPosArr do
(
point pos:p wirecolor:yellow
)
for i = 2 to pointsPosArr.count do
(
format "dist[%:%]= %\n" (i-1) i (distance pointsPosArr[i] pointsPosArr[i-1])
)
)That’s bisection!
Note: I don’t really understand well your method, but my cursor icon gets mad when the script finish. And if I save the scene and reload it, the cursor’s still mad. I’m with 3dsMax 2016. !!??
Upps! My solution is only valid for splines with nearly-straight segments or distance smaller than knots distances. If not, we have to subdivide segments.
I’ll write the code later…
It’s an INTERESTING CHALLENGE !
as soon as i have a time i will try to give my solution.
so, the challenge’s rule is the same: DO FAST AND SAVE MEMORY
Here’s the solution with subSegments for splines with very closed segments. I don’t think you’ll need more than 10 subsegments for really extrange splines.
This solution is coded with a struct, so more memory and time than with arrays, but more clear. If you want the array solution, I have it.
I get 2ms for your spline (memory 28680L) with 5 subsegments (they could be just 1 for this case) and an accuracy of 0.0001.
(
gc()
t1 = timeStamp()
m1 = heapfree
-- Catched functions
local interpCurve = interpCurve3D
local interpBezier = interpBezier3D
-- Input Data
curSpline = selection[1]
fixedDist = 33
numSubSeg = 5 -- Caution!!! Minimum 1
accuracy = 0.0001
-- Basic spline data for calculation
numK0 = numknots curSpline 1
closed = isClosed curSpline 1
if closed do numK0 +=1
numK = (numK0 - 1) * numSubSeg + 1
numSeg = numSegments curSpline 1
invNumSeg = 1.0 / numSeg
invNumSubSeg = 1.0 / numSubSeg
relStep = invNumSubSeg * invNumSeg
---------------------------------------
-- Data for each knot
struct Knot (coord, segment, relParam)
local knots = #()
local coord
local segment
local absParam
local relParam
ptsCounter = 0
for i = 1 to numK0 - 1 do
(
ptsCounter += 1
coord = getKnotPoint curSpline 1 i
segment = i - 1
absParam = invNumSeg * (i-1)
relParam = 0.0
knots[ptsCounter] = Knot coord segment relParam
for j = 1 to numSubSeg - 1 do
(
ptsCounter += 1
segment = i
absParam += relStep
relParam += invNumSubSeg
coord = (in coordsys world (interpCurve curSpline 1 absParam pathParam:true))
knots[ptsCounter] = Knot coord segment relParam
)
)
ptsCounter += 1
if closed then
(
coord = getKnotPoint curSpline 1 1
)
else
(
coord = getKnotPoint curSpline 1 numK0
)
knots[ptsCounter] = Knot coord numSeg 1.0
--------------------------------------
-- Calculation
pointsPosArr = #(knots[1].coord)
stopLoop = false
currentKnotIdx = 2
while stopLoop == false do
(
-- Get index of knot farthest than fixedDist from previous one
lastPoint = pointsPosArr[pointsPosArr.count]
morePoints = false
for i = currentKnotIdx to numK while not morePoints do
(
dist = distance lastPoint knots[i].coord
currentKnotIdx = i
if dist >= fixedDist do
(
morePoints = true
)
)
-- Calculation of the point by bisection (max 1000 iterations)
if morePoints then
(
segmentID = knots[currentKnotIdx].segment
pt
error = 1e6
a = knots[currentKnotIdx - 1].relParam
b = knots[currentKnotIdx].relParam
if b == 0.0 do b = 1.0
iterations = 0
while error > accuracy and iterations < 1000 do
(
iterations += 1
param = (a+b) * 0.5
pt = interpBezier curSpline 1 segmentID param pathParam:true
dist = distance lastPoint pt
if dist > fixedDist then b = param else a = param
error = abs(dist - fixedDist)
)
append pointsPosArr pt
)
else
(
stopLoop = true
)
)
t2 = timeStamp()
m2 = heapfree
format "Time: %ms; Mem: %\n" (t2-t1) (m1-m2)
-- Print and Plot results
for p in pointsPosArr do
(
point pos:p wirecolor:yellow
)
for i = 2 to pointsPosArr.count do
(
format "dist[%:%]= %\n" (i-1) i (distance pointsPosArr[i] pointsPosArr[i-1])
)
)Hope it helps.