[Closed] (SDK) what is equivalent to mxs nearestpathparam?

Hi DenisT.

Did you solve this?
I’m fighting with a plugin script modifier and I have a serious time bottleneck with this function (proyecting all mesh verts against a spline).
I’m wondering if this rutine could be done in C++ and compile it ‘on the fly’.

(P.S.: stupid question. Of course you’ve solved it, as allways! :bowdown: )

i couldn’t find any sdk method to make it easy. so i do distance comparison with precalculated step points. they are cached in polyline. it works good enough in my case

I’ve been thinking (and working) on this subject for two months: if DenisT has a problem, it must be a real-interesting-passioning challenge! And perhaps I can help!?

How to solve this?
Let’s back to University, with all extrange functions for interpolation, solving roots, …

If we get a function that fits the spline, then it’s seems easy: let’s call Q the external point.
1- Find all spline points P whose tangent is perpendicular to the [Q ,P] vector;
2- Calc the distance of [Q,P] vector
3- Select the smallest of all

The first point reduces to calculate the function points where:
dot_product [Q,P] [Tangent in P] = 0, being [Tangent in P] the derivative of the function in P.

There are several methods to interpolate splines according to the case. Most used and simplest are third degree polynomial interpolation by segments: for each segment of the spline, you find a third degree polynomial that meets some restrictions, for example containing the extreme knots of the segment and having the same tangent at these knots.

This starts to become a problem… if we fit the spline with a third degree polynomial (the simplest one possibility), the derivative is a second degree polynomial, so the dot product is a fifth degree function… and by the Abel-Ruffini theorem, we know that there’s no a general formula to solve this.

[… to be continued]

Luckely, not all is lost.

Third degree interpolation methods by segments are parametric in the variable ‘t’ which goes from 0 at start knot to 1 at the end knot.

If there’s a solution for our fifth-degre equation (dot product = 0), then it must be between 0 and 1.
Here appears the Newton–Raphson method. It is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function in a known interval. The convergence is at least quadratic in a neighbourhood of the zero (that means converges very fast).

So I started with the Hermite interpolation:
Unit interval (0, 1)
On the unit interval (0,1), given a starting point P0 at t=0 and an ending point P1 at t=1 with starting tangent m0 at t=0 and ending tangent m1 at t=1, the polynomial can be defined by

P(t) = (2t^3-3t^2+1)P0 + (t^3-2t^2+t)m0 + (-2t^3+3t^2)P1 +(t^3-t^2)m1

After programming it, the function didn’t fit fine Max splines. In fact, the function depends on another parameter that gives de ‘weight’ of the curve. And this weight is not the same for all segments.

Then I found the Centripetal Catmull-Rom interpolation, that I didn’t knew before, that seems to be used in computer graphics for splines. That sounds nice!

https://en.wikipedia.org/wiki/Centripetal_Catmull–Rom_spline

The only problem is that you need 4 points to define a segment as it uses the external points to find the tangent. Thus, I had to search a start and an end imaginary knots for the spline, using tangent given by 3DSMAX at these starting/ending knots.

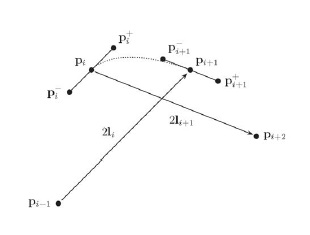
The general formula is:
F(t) = (-0.5t + t^2 – 0.5t^3)P0 + (1 – 2.5t^2 + 1.5t^3t)P1 + (0.5t + 2t^2 – 1.5t^3)P2 + (-0.5t^2 + 0.5t^3)*P3

Bingo!! That fits very fine the spline and the ‘t’ param is very close to the 3DSMAX ‘pathparam’ (non uniform) for splines.

Next Chapter: “how to make it faster (1)”

What I used in a first round to speed up the function is:

• Make two cycles, with a first one of at least 7 subdivisions for each spline segment to find the ‘zone’ where the nearestPoint is and a second sub-subdivision just in this zone to avoid calculate all the spline sub-subdivided.
  Why 7 subdivisions? As there can be segments like segment 3 in the image below, I think 7 is a needed minimum.

• Reduce Newton-Raphson iterations to 10 (if accuracy is not reached before)

• Take two accuracies: one for the first cycle and a smallest one for the second.

• Check for straight segments (comparing its length to the distance between its extreme knots) to make the exact (and quick) calculation through vertex projection instead of Catmull-Rom interpolation.

• Simplify Catmull-Rom coefficients to At^3+Bt^2+C*t+D, so you can reuse those coefficients in first and second derivative that you will need for the calc.

• Create initial array for these coefficients and knots, and check allways if the elements are allready calculated to avoid recalc something.

• Learn a little bit of C# and Max SDK to write the function in a compiled languaje!!!

P.S.: I don’t know if there is someone interested in this thread, but I’ll go on with it.

[Next… problems, how to make it faster (2) and, finally, code]

I wonder why you have decided to work with Catmull-Rom spline with 4 "imaginary" control points instead of Bezier spline and getInVec() - getOutVec().

No, I haven’t explained well.
The Centripetal Catmull-Rom uses the knots of the spline. But as it needs 4 knots to define 1 segment, you have a problem with the first and the last segments of the spline (S-1 & S-6 in the image above).
So you have to create an additional first vert and an additional last vert. I’ve done it with tangents at this points but you are right I could have use the inVect for the first and the outVect for the last one.

By the way, thanks for following!

But, in fact, there’s a need of more subdivisions near bezier corner knots that perhaps using outVec can be reduced. You are wellcome to improve the code :keenly:

Further more, you need to find an analytical function to be able to derive it twice. That’s not the case with most bezier splines that aren’t. You get values iterating.
In fact, viewing the results of the maxscript function ‘nearestpathparam’ and others, 3ds Max splines mustn’t have an analitical expression. That’s why you need the parameter ‘steps’ in some functions to set the number of iterations.